Flory-Rehner Theory
of Polymer Network Swelling

The thermodynamics of swelling of network structures was first investigated by Paul Flory and J. Rehner in the early 1940s.^1-3 They developed a model that describes the isotropic swelling of rubber crosslinked in the dry state. Their model was later extended by Stephen Bruck to include anisotropic networks.⁴

A three-dimensional network polymer such as vulcanized rubber may absorb large amounts of liquid when exposed to a compatible diluent. Under these conditions, swelling of the network will occur and an elastic retractive force develops. The driving force of the swelling process is mainly enthalpic in nature. As the volume of the network increases the chains are stretched which, in turn, causes a decrease in entropy because the extended configuration of the chains is less likely. Thus, an elastic retractive force develops. An equilibrium is eventually reached when the two opposing forces become equal.

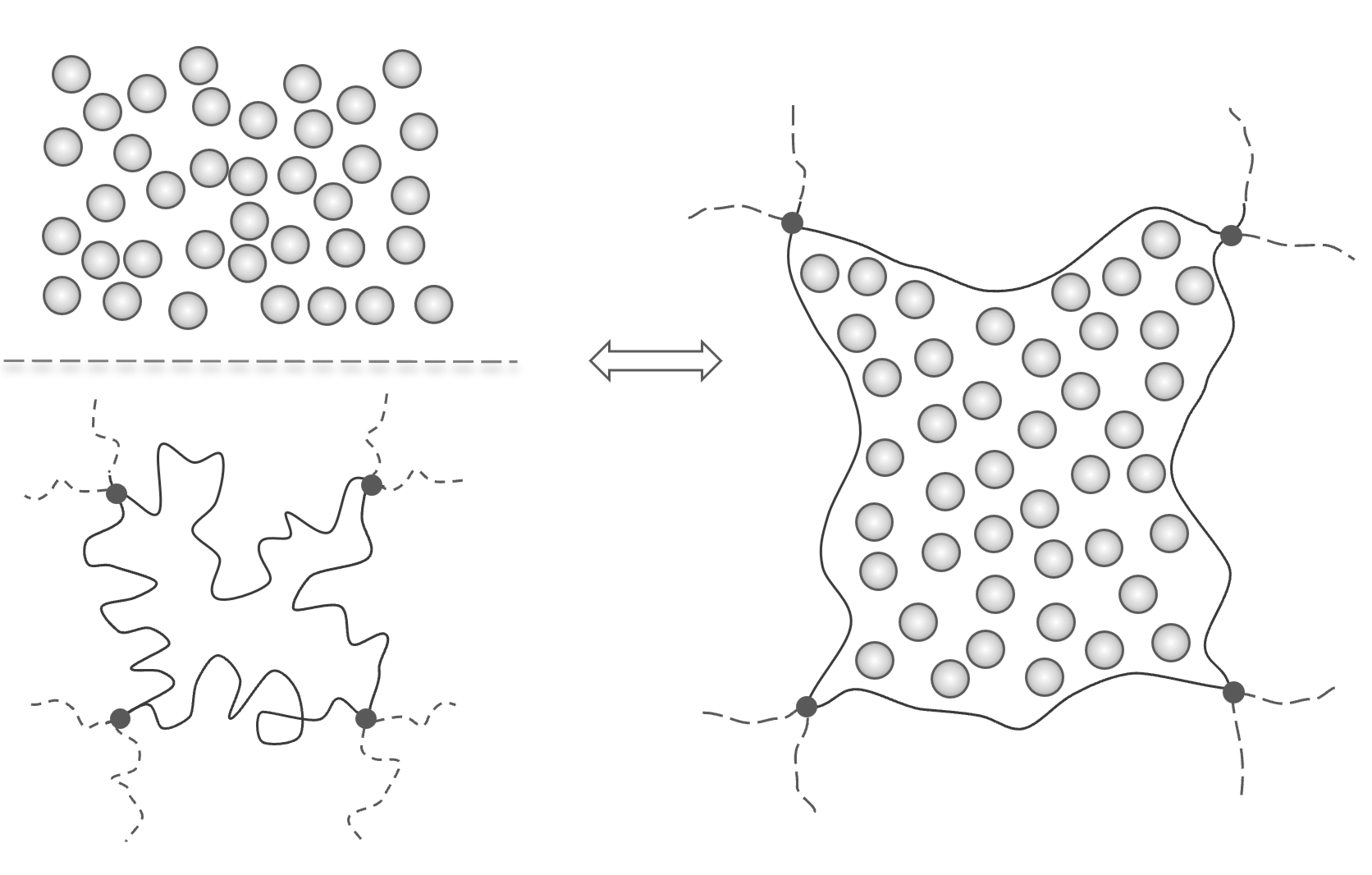
Flory and Rehner assumed that the elastic (ΔF_el) and mixing (ΔF_mix) contributions to the free energy of swelling of dry polymer networks are separable and additive:

ΔF = ΔF_mix - ΔF_el

where ΔF is the total free energy change involved in the mixing of pure solvent with the crosslinked network, ΔF_mix is the free energy of mixing, and ΔF_el is the elastic free energy. The free energy change on mixing, ΔF_mix, can be calculated with the Flory-Huggins lattice theory. Assuming one single network polymer molecule, the number of individual polymer molecules can be set zero, N_p = 0. Then the free energy of mixing maybe written

ΔF_mix / kT ≈ N_s ln φ_s + χ_ps N_s φ_p

where N_s is the number of solvent molecules and φ_s and φ_p are the volume fractions of the solvent and polymer in the polymer network, respectively.⁵

By analogy with the elasticity of rubbers, the deformation process during swelling is assumed to occur without appreciable change in internal free energy of the polymer network. Then according to the statistical theory of rubber elasticity we may write

ΔF_el = (VnkT / 2) · [α_x² + α_y² + α_z² - 3 - ln(α_xα_yα_z)]

where V is the volume of the rubber cube, n is the number of network subchains per unit volume, i.e. the number of chains between crosslinks, and α_i = R_i / R_i,0 are the extension ratios of the rubber strands in the three principal directions, e_x, e_y, e_z. In the case of two-dimensional isotropy, such as in crosslinked fibers, α_x ≠ α_y = α_z. With α = α_y = α_z the expression above simplifies to

ΔF_el = (VnkT / 2) · [2α² + α_x²  - 3 - ln(α_xα²)]

and for a fully isotropic polymer network, α_x = α_y = α_z:

ΔF_el = (VnkT / 2) · [3α² - 3 - ln α³]

To determine the crosslink density, the weight of the swollen (V) and unswollen network (V₀) at equilibrium is measured. From a knowledge of the densities of the solvent and polymer, one can calculate q = V / V₀. Assuming that mixing occurs without an appreciable change in the total volume of the system (polymer plus solvent), the deformation factor for an isotropic polymer network may be written

α³ = 1 / φ_p = (V₀ + N_s v_s) / V₀

It follows that

(∂α / ∂N_s)_T,p  = v_s / 3α²V₀

where v_s is the volume of a solvent molecule. The swelling equilibrium is reached when the chemical potential of the solvent in the swollen network μ_s is equal to that of the pure solvent μ_s⁰. At this point, the polymer volume fraction has the value φ_p = φ_p,m. The chemical potential of the solvent in the swollen polymer network is given by

(μ_s - μ_s⁰) = (∂ΔF_el / ∂α)_T,p (∂α / ∂N_s)_T,p + (∂ΔF_mix / ∂N_s)_T,p

Evaluating all three derivatives yields

(μ_s - μ_s⁰) / RT = ln φ_s + φ_p + χ_ps φ_p² + (v_s / 3α²V₀) (Vn/ 2) · [6α - 3/α]

and with (μ_s - μ_s⁰) / RT = 0

 ln (1 - φ_p,m) + φ_p,m + χ_ps φ_p,m² = - (v_s ν_e / V₀) · [φ_p,m^1/3 - φ_p,m/2]

where ν_e = Vn = M / M_c is the effective number of chains in the network, M_c is the (average) molecular weight between crosslinks, and M is the mass of the rubber cube.

At low degree of crosslinking, i.e. at large M_c, φ_p,m^1/3 is considerably larger than  φ_p,m /2. Then as a first approximation, the second term of the right-hand side may be neglected. Expanding the logarithm on the left-hand side and neglecting higher terms in the series expansion, results in an equation that can be easily solved. The result is the Flory-Rehner expression for isotroplc swelling of rubber:

ν_e = (V₀ φ_p,m^5/3) · (1/2 - χ_ps ) / v_s

For nonpolar systems, the interaction parameter χ_ps can be expressed in terms of solubility parameters:

ν_e = (V₀ φ_p,m^5/3) · {(2 v_s)^-1 - (δ_s - δ_p )² / RT}

If we know the molar volume of the solvent v_s, and the Flory-Huggins interaction parameter χ_ps (or solubility parameters of the solvent and polymer) and measure the volume of the swollen and unswollen polymer network at its equilibrium, the effective crosslink density ν_e may be calculated.

References & Notes

1. P.J. Flory and J. Rehner, J. Chem. Phys., 11, 521 (1943)

2. P. J. Flory, J. Chem. Phys. 18, 521 (1943)

3. Paul L. Flory, Principles of Polymer Chemistry, Ithaca, New york, 1953

4. S. D. Bruck, J. of Research of the National Bureau of Standards, A. Physics and Chemistry, Vol. 65A, No.6 (1961)

5. χ_ps is the so called Flory-Huggins interaction parameter. It describes the polymer-solvent interaction:

   χ_ps = ΔH_mix / (kT N_s φ_p)

6. If we assume that the cross-interaction energy is the geometric average of the interaction energies of the pure components, and that the molar volume of the solvent and polymer are identical, then the interaction parameter can be estimated with (see Hildebrand-Scott theory)

   χ_H ≈ v_s (δ_p - δ_s)² / RT